今回の記事ではExtended Kalman Filter(EKFと略します)を用いてLorenz96モデルのデータ同化を行います。
この記事での計算はJulia1.3、Junoを使用しています。 JunoはJupyter Notebookと使い勝手が変わらない上に、出力ファイルや変数の中身を簡単に見れて便利です。Junoの導入についてはJulia のIDE Juno を使って快適なJuliaとの生活をする手引き(前半)が参考になります。
Julia言語は素人なので、こう書くとよいなどありましたら教えていただけると助かります。なお、Plotsの使い方があまりにも分からないので、ファイルに出力して描画にはgnuplotを使用しています。
Extended Kalman Filter
Kalman Filterのモデル$M$が非線形の場合への拡張がExtended Kalman Filterです。 モデル誤差のない、完全モデルを仮定します。1
導出
最小分散推定としてExtended Kalman Filterの式を導出します2。数学科向けに書いているので、正直に追わなくても式だけ覚えれば支障はないと思います。
$(\Omega,\mathcal{F},P)$を確率空間とし、$\varepsilon_i^o:\Omega \to \mathbb{R}^{d},\quad i=1,2,\ldots$を平均が$0$、共分散行列$R_i$の$d$次元二乗可積分確率変数列とします。 また、時間発展モデル$M:\mathbb{R}^N \to \mathbb{R}^N$を$C^1$級写像とし、真値$x_i^t \in \mathbb{R}^N \quad i=0,1,\ldots$が与えられているとします。さらに、$H_i \in M(d,N),\quad i=1,2,\ldots$3を用いて
\begin{align}
y_i^o &= H_i x_i^t + \varepsilon_i^o \quad i = 1,2,\ldots \
x_{i+1}^t &= M(x_i^t),\quad i=0,1,\ldots
\end{align}
という関係式が成り立っていることを仮定します。最後に$\varepsilon_0^a:\Omega \to \mathbb{R}^N$という平均$0$、共分散行列$P_0^a$の$N$次元二乗可積分確率変数を用いて初期値を$x_0^a = x_0^t + \varepsilon_0^a$と定めます。以上の仮定の下で、いくつかの近似を用いて帰納的に予報値$x_i^f$と解析値$x_i^a$を$i=1,2,\ldots$に対して構成します。
$i=1$のとき、$x_1^f = M(x_0^a)$とします。予報誤差共分散$P_1^f$を$\varepsilon_1^f := x_1^f-x_1^t$の共分散行列とするとき、
\begin{align}
x_1^f &= M(x_0^t + \varepsilon_0^a) \
&= M(x_0^t) + JM_{x_0^t} \varepsilon_0^a \
&= x_1^t + JM_{x_0^a} \varepsilon_0^a
\end{align}
が$\varepsilon_0^a$の二次以上の項を無視する近似で成立するので、
\begin{align} P_1^f = JM_{x_0^a} P_0^a JM_{x_0^a}^{\top} \end{align}
と求まります。 $x_1^a$は、重み行列$K_1 \in M(N,d)$(Kalman Gain Matrixと言います)を用いて
\begin{align} x_1^a = x_1^f + K_1 (y_1^o - H_1 x_1^f) \end{align}
という形で表されるとし4、重み$K_1$は最小分散推定によって定めます。すなわち、$\varepsilon_1^a := x_1^a-x_1^t$の共分散行列を$P_1^a$とするとき、$tr(P_1^a)$を最小にするように定めます。
\begin{align}
x_1^a &= x_1^t + \varepsilon_1^f + K_1 (H_1 x_1^t + \varepsilon_1^o - H_1 x_1^t - H_1 \varepsilon_1^f) \
&= x_1^t + (I - K_1 H_1)\varepsilon_1^f + K_1 \varepsilon_1^o
\end{align}
となり、$\varepsilon_1^f ,\varepsilon_1^o$の相関が$0$であるという近似のもと \begin{align} P_1^a = (I - K_1 H_1)P_1^f (I-K_1 H_1)^{\top} + K_1 R_1 K_1^{\top} \end{align}
として求まります。これから$tr(P_1^a)$を$K_1$の関数として微分して$0$になる事を課すと、面倒な計算5の後に
\begin{align} K_1 = P_1^f H_1^{\top} (H_1 P_1^f H_1^{\top} + R_1)^{-1} \end{align} として求まります。これを$P_1^a$に代入して計算すると \begin{align} P_1^a = (I - K_1 H_1)P_1^f \end{align} となります。以上の手続きを$i=2,3,\ldots$として全く同様に繰り返します。
アルゴリズム
$x_0^a,P_0^a$を適当に与えておいて、$i=1,2,\ldots$に対して、 モデル$M$による時間発展で少し未来の情報を得るForecast Step
\begin{align}
x_i^f &= M(x_{i-1}^a) \
P_i^f &= JM_{x_{i-1}^a} P_{i-1}^a JM_{x_{i-1}^a}^{\top}
\end{align}
予報値$x_i^f$と観測値$y_i^o$の重み付き平均で最適な推定値を求めるAnalysis Step
\begin{align}
K_i &= P_i^f H_i^{\top} (H_i P_i^f H_i^{\top} + R_i)^{-1} \
x_i^a &= x_i^f + K_i (y_i^o - H_i x_i^f) \
P_i^a &= (I - K_i H_i)P_i^f
\end{align}
を交互に繰り返します。
設定
以下の数値計算では、L96モデル
\begin{align}
\frac{\mathrm{d}u_i}{\mathrm{d}t} = (u_{i+1} - u_{i-2})u_{i-1} - u_{i} + F,\quad i=1,\ldots,N \
u_i = u_{N+i}(i\leq 0),u_j=u_{j-N}(j>N)
\end{align}
を$N=40$として4段4次Runge-Kutta法で数値的に時間発展させる写像を$M$とします。$x_{i+1}^t=M(x_i^t), i=1,2,\ldots$として真値を生成し、真値の各成分に標準正規分布に従う乱数を加えた観測値を作ります。このとき$H_i = I,R_i = I$となります。
真値と観測データの生成
先に全体のコードを書いてから細かく解説します。
L96_truestate.txtに真値を保存し、L96_observation.txtに真値の各成分に標準正規分布に従う乱数を加えた観測値を保存するプログラムです。
using LinearAlgebra
using Statistics
using DelimitedFiles
using Random
##L96modelの右辺
function L96(u;F=8.0,N=40)
f = fill(0.0, N)
for k in 3:N-1
f[k] = (u[k+1]-u[k-2])u[k-1] - u[k] + F
end
f[1] = (u[2]-u[N-1])u[N] - u[1] + F
f[2] = (u[3]-u[N])u[1] - u[2] + F
f[N] = (u[1]-u[N-2])u[N-1] - u[N] + F
return f
end
#4-4Runge-Kutta
function Model(u;dt=0.05)
du = u
s1 = L96(u .+ dt)
s2 = L96(u + s1*dt/2)
s3 = L96(u + s2*dt/2)
s4 = L96(u + s3*dt)
du += (s1 + 2*s2 + 2*s3 + s4)*(dt/6)
return du
end
function main()
Time_Step = 14600
F = 8.0
N = 40
u = fill(F,N) + rand(N)
##一年分はスピンアップとして捨てる
for i in 1:Time_Step
u = Model(u)
end
##一年分を真値として保存
open("L96_truestate.txt","w") do truestate
for i in 1:Time_Step
u = Model(u)
writedlm(truestate, [(i/40) u'])
end
end
##真値にノイズを足して観測データを作る
u_true = readdlm("L96_truestate.txt")
open("L96_observation.txt","w") do observation
for i in 1:Time_Step
writedlm(observation, [(i/40) (u_true[i,2:N+1]+randn(N))'])
end
end
end
main()
時間発展写像Mの記述
##L96modelの右辺
function L96(u;F=8.0,N=40)
f = fill(0.0, N)
for k in 3:N-1
f[k] = (u[k+1]-u[k-2])u[k-1] - u[k] + F
end
f[1] = (u[2]-u[N-1])u[N] - u[1] + F
f[2] = (u[3]-u[N])u[1] - u[2] + F
f[N] = (u[1]-u[N-2])u[N-1] - u[N] + F
return f
end
#4-4Runge-Kutta
function Model(u;dt=0.05)
du = u
s1 = L96(u)
s2 = L96(u + s1*dt/2)
s3 = L96(u + s2*dt/2)
s4 = L96(u + s3*dt)
du += (s1 + 2*s2 + 2*s3 + s4)*(dt/6)
return du
end
4段4次Runge-Kutta法でdt=0.05(気象データの6時間に相当)だけ時間発展させます。
解くだけならライブラリを使う方が良いですが、時間発展の幅の調整や、接線形コードを後に書く都合上、ベタに実装しています。
関数L96で方程式の右辺の関数を実装し、Modelで時間発展させます。
真値の生成
Time_Step = 14600
F = 8.0
N = 40
u = fill(F,N) + rand(N)
##一年分はスピンアップとして捨てる
for i in 1:Time_Step
u = Model(u)
end
##一年分を真値として保存
open("L96_truestate.txt","w") do truestate
for i in 1:Time_Step
u = Model(u)
writedlm(truestate, [(i/40) u'])
end
end
Time_Stepは一年分の時間反復回数です。dt=0.05が六時間に相当するのでここから一年分の反復回数を計算できます。初期値は何でもいいので平衡点$(F,F,\ldots,F)$に乱数を足して作っています。一年分の時間発展をアトラクターに達するまでとして捨てています。アトラクター外の点はModelで時間発展させるとアトラクターに漸近しようとするので、誤差が減少します。それではデータ同化をする意味が無いです。
数値データのファイルへの読み書きにはusing DelimitedFilesとすると使えるwritedlmやreaddlmを使っています。writedlm(truestate, [(i/40) u'])で時刻(日)を1列目に、2~N+1列目にuの成分をu'として横に並べて出力します。
観測データの生成
##真値にノイズを足して観測データを作る
u_true = readdlm("L96_truestate.txt")
open("L96_observation.txt","w") do observation
for i in 1:Time_Step
writedlm(observation, [(i/40) (u_true[i,2:N+1]+randn(N))'])
end
end
readdlmで先ほど作ったL96_truestate.txtの数値を行列に保存します。6
あとは先ほどと同様にwritedlm(observation, [(i/40) (u_true[i,2:N+1]+randn(N))'])で各成分に標準正規分布に従う乱数を加えたものを書き出し、L96_observation.txtに保存します。
Extended KFの実装
コードを示してから解説します。
L96_EKF_output_noinflation.txtに$tr(P^a)$と予報値のRMSE、観測値のRMSEを出力するプログラムです。
using LinearAlgebra
using Statistics
using DelimitedFiles
##L96modelの右辺
function L96(u;F=8.0,N=40)
f = fill(0.0, N)
for k in 3:N-1
f[k] = (u[k+1]-u[k-2])u[k-1] - u[k] + F
end
f[1] = (u[2]-u[N-1])u[N] - u[1] + F
f[2] = (u[3]-u[N])u[1] - u[2] + F
f[N] = (u[1]-u[N-2])u[N-1] - u[N] + F
return f
end
#4-4Runge-Kutta
function Model(u;dt=0.05)
du = u
s1 = L96(u)
s2 = L96(u + s1*dt/2)
s3 = L96(u + s2*dt/2)
s4 = L96(u + s3*dt)
du += (s1 + 2*s2 + 2*s3 + s4)*(dt/6)
return du
end
function main()
Time_Step = 14600
N = 40
M = 40
F = 8.0
IN = Matrix(1.0I, N, N)
delta = 1.0e-5
u_true = readdlm("L96_truestate.txt")
u_obs = readdlm("L96_observation.txt")
H = Matrix(1.0I, M, N)
R = Matrix(1.0I, M, M)
open("L96_EKF_output_noinflation.txt", "w") do output
ua = rand(N) .+ F
for i in 1:Time_Step
ua = Model(ua)
end
Pa = 25.0 * IN
for i in 1:Time_Step
##forecast step
uf = Model(ua)
JM = zeros(N,N)
for j in 1:M
JM[:,j] = (Model(ua+delta*IN[:,j]) - Model(ua))/delta
end
Pf = JM * Pa * JM'
##analysis step
K = Pf * H' * inv(H*Pf*H' + R)
ua = uf + K*(u_obs[i,2:N+1] - H*uf)
Pa = (I - K*H)Pf
##output
writedlm(output, [(i/40) sqrt(tr(Pa)/N) (norm(u_true[i,2:N+1] - uf)/sqrt(N)) (norm(u_obs[i,2:N+1] - u_true[i,2:N+1])/sqrt(N))])
end
end
end
main()
パラメータの設定
Time_Step = 14600
N = 40
M = 40
F = 8.0
IN = Matrix(1.0I, N, N)
delta = 1.0e-5
u_true = readdlm("L96_truestate.txt")
u_obs = readdlm("L96_observation.txt")
H = Matrix(1.0I, M, N)
R = Matrix(1.0I, M, M)
M=40は観測の次元で、ここではNと同じです。ここを変えるときはHの形も合わせて変えるようにしてください。
IN = Matrix(1.0I, N, N)とdelta = 1.0e-5は後にヤコビ行列JMの計算に使うためのものです。
u_true = readdlm("L96_truestate.txt")とu_obs = readdlm("L96_observation.txt")で真値と観測を行列にして取り込みます。u_trueは計算結果を評価するためのもので、EKFの計算には使いません。
HとRは今回の設定では単位行列です。
初期化
ua = rand(N) .+ F
for i in 1:Time_Step
ua = Model(ua)
end
Pa = 25.0 * IN
uaの初期値をアトラクター上の点から適当に一つ取ることにします。Paの初期値は単位行列の25倍としておくのが一般的かと思います。
Forecast Step
\begin{align}
x_i^f &= M(x_{i-1}^a) \
P_i^f &= JM_{x_{i-1}^a} P_{i-1}^a JM_{x_{i-1}^a}^{\top}
\end{align}
##forecast step
uf = Model(ua)
JM = zeros(N,N)
for j in 1:M
JM[:,j] = (Model(ua+delta*IN[:,j]) - Model(ua))/delta
end
Pf = JM * Pa * JM'
モデル$M$の$x=u^a$におけるヤコビ行列JMの計算が問題で、本当はModelの接線形コードを書くのが筋ですが、説明が長くなるのでここでは簡単に偏導関数の定義式
\begin{align}
\frac{\partial f}{\partial x_i} (x) := \lim_{\delta \to 0} \frac{f(x+\delta e_i)-f(x)}{\delta}
\end{align}
を近似計算することにします。deltaが小さい方が精度が良いですが、あまり小さくしすぎると桁落ちが起きて精度が逆に悪化します。
Analysis Step
\begin{align}
K_i &= P_i^f H_i^{\top} (H_i P_i^f H_i^{\top} + R_i)^{-1} \
x_i^a &= x_i^f + K_i (y_i^o - H_i x_i^f) \
P_i^a &= (I - K_i H_i)P_i^f
\end{align}
##analysis step
K = Pf * H' * inv(H*Pf*H' + R)
ua = uf + K*(u_obs[i,2:N+1] - H*uf)
Pa = (I - K*H)Pf
ほぼそのまま書けます。u_obs[i,2:N+1]としているのは一列目に時刻が入っているからです。
using LinearAlgebraをしてからIを使うと計算式から単位行列のサイズを勝手に判断してくれます。かしこい。
出力
writedlm(output, [(i/40) sqrt(tr(Pa)/N) (norm(u_true[i,2:N+1] - uf)/sqrt(N)) (norm(u_obs[i,2:N+1] - u_true[i,2:N+1])/sqrt(N))])
Paのトレースsqrt(tr(Pa)/N)と予報値から計算したRMSE(norm(u_true[i,2:N+1] - uf)/sqrt(N)および観測から計算したRMSE(norm(u_obs[i,2:N+1] - u_true[i,2:N+1])/sqrt(N))を出力します。
観測から計算したRMSEが時間平均して1となるように規格化し、他の量はそれにスケールを合わせています。
Covariance Inflation
結果をグラフにすると下のようになります。
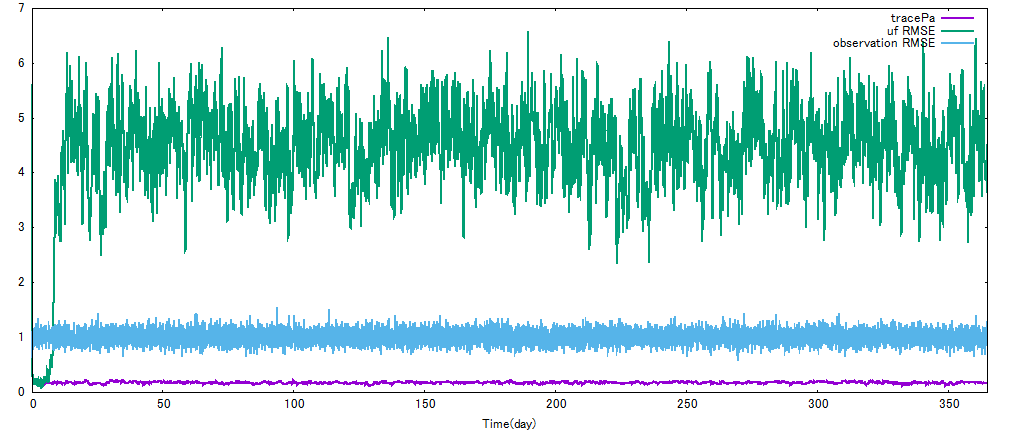
あれ、何だか上手くいってない… 観測のRMSE(水色)より予報値のRMSE(緑)が下がらないと意味がないのですが、全然下がってません。最初は上手くいってるのに。tracePa(紫)はずっと下がったままなんですが…
実は上手くいかないのはプログラムのミスではなく仕様です。最小分散推定としては上手くいっていることがtracePaが小さいことからも分かるのですが、だからと言ってちゃんと真値の周りに行ってくれるわけではないのです。この現象をFilter Divergence7と言い、多くのデータ同化手法に付きまといます。原因は予報値をあまりにも信用しすぎていることです。図で説明します。
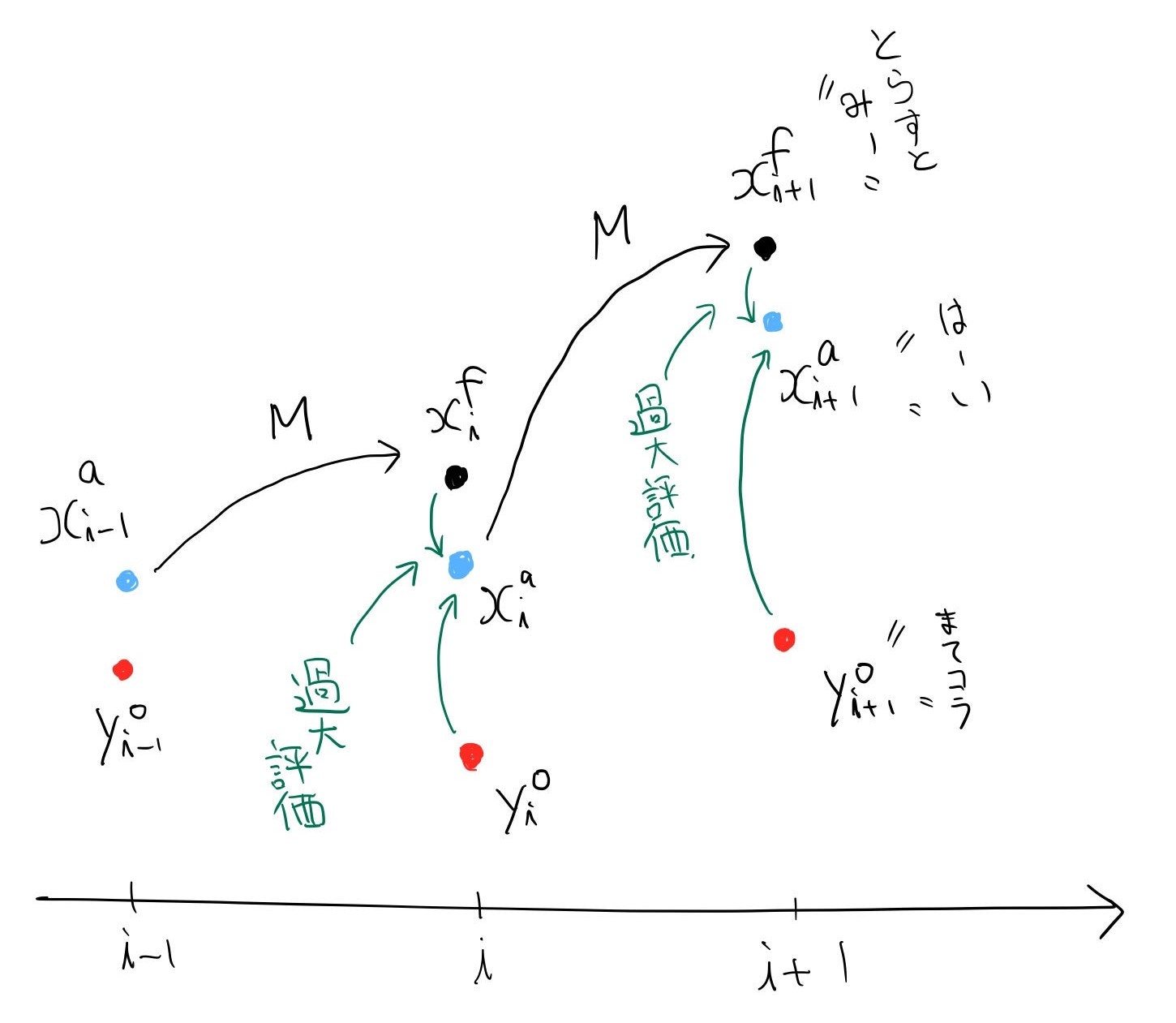
解析値$x_i^a$は予報値$x_i^f$と観測値$y_i^o$の適切な重み付き平均によって求められるのですが、予報誤差共分散$P_i^f$を過少に見積もると予報値$x_i^f$を”誤差が小さい良いやつだ!”と過大評価して観測を無視しがちになります。そうすると$M$で何度も予報値を時間発展することになり、誤差が膨らんで使い物にならなくなってしまうわけです。
これを防ぐには$P_i^f$の過少評価をただせばいいわけで、次のようにForecast Stepを書き換えます。
##forecast step
uf = Model(ua)
JM = zeros(N,N)
for j in 1:M
JM[:,j] = (Model(ua+delta*IN[:,j]) - Model(ua))/delta
end
Pf = 1.1 * JM * Pa * JM'
違いはPf = 1.1 * JM * Pa * JM'として1.1倍しただけです。
これで計算しなおした結果を下に示します。
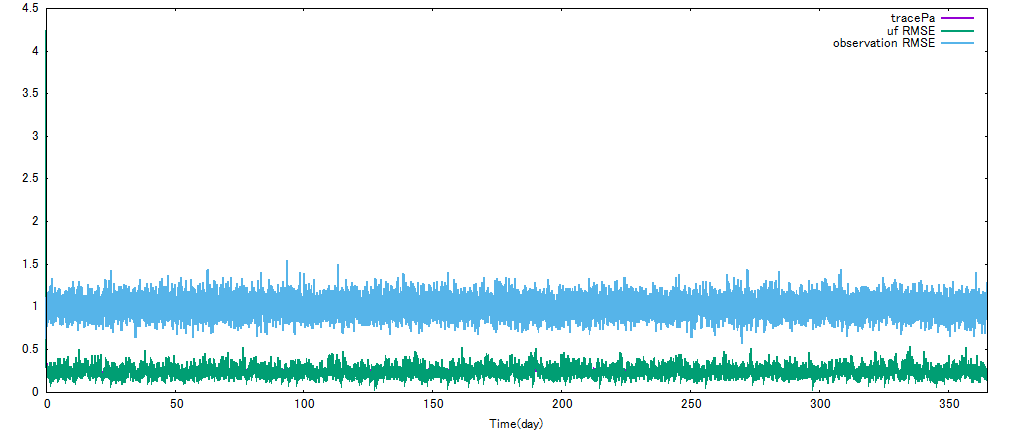
無事に水色よりも緑の線が下に来ました。成功です。RMSEはおおよそ0.2程度まで落ちます。
Pf = 1.1 * JM * Pa * JM'の1.1はInflation Parameterといい、本来手で調整して一番結果が良くなる値を探さなければなりません。いろいろやってみるといいと思います。
まとめ
今回はEKFを解説しました。 観測の次元を変更した場合をそのうち追記します。
EKFは予報誤差共分散$P^f$の計算が重いほか、そもそも$N\times N$行列を陽に保存することができないなどの事情があって大自由度の系では使われません。それでもKalman Filterの最も素直な非線形拡張なので紹介しました。
次回は3次元変分法かEnKFになると思います。
-
モデル誤差のある場合への式の拡張は難しくなく、どちらかというとモデル誤差を推定する方が難しいです。 ↩
-
最尤推定としての導出など数学的にまとまっているのは”An Introduction to Estimation Theory”, Stephen E. Cohnでしょう。吉田数理統計学辺りを参照しながら読むと良いと思います。 ↩
-
$M(d,N)$で$d\times N$行列全体を表します。 ↩
-
$H_1 = I$なら本当に重みのような形です。$M$が線形で$\varepsilon_i^o$がすべて正規分布に従うならば、最尤推定で自動的にこの形に決まります。今回はそういう仮定が無いので、この形になる事を仮定します。あるいは、線形正規で近似していると思うこともできます。 ↩
-
Sherman-Morrisonの公式とか使います。 ↩
-
一行づつ読み取る方法が調べても分からなかったので誰か教えていただけると助かります。 ↩
-
“Concrete ensemble Kalman filters with rigorous catastrophic filter divergence.”, Kelly, Majda AJ, Tong.なんかも参考になると思います ↩